2597. Cycle Length Queries in a Tree

You are given an integer n. There is a complete binary tree with 2n - 1 nodes. The root of that tree is the node with the value 1, and every node with a value val in the range [1, 2n - 1 - 1] has two children where:

• The left node has the value 2 * val, and
• The right node has the value 2 * val + 1.

You are also given a 2D integer array queries of length m, where queries[i] = [ai, bi]. For each query, solve the following problem:

1. Add an edge between the nodes with values ai and bi.
2. Find the length of the cycle in the graph.
3. Remove the added edge between nodes with values ai and bi.

Note that:

• A cycle is a path that starts and ends at the same node, and each edge in the path is visited only once.
• The length of a cycle is the number of edges visited in the cycle.
• There could be multiple edges between two nodes in the tree after adding the edge of the query.

Return an array answer of length m where answer[i] is the answer to the ith query.

Example 1:

Input: n = 3, queries = [[5,3],[4,7],[2,3]]
Output: [4,5,3]
Explanation: The diagrams above show the tree of 23 - 1 nodes. Nodes colored in red describe the nodes in the cycle after adding the edge.
- After adding the edge between nodes 3 and 5, the graph contains a cycle of nodes [5,2,1,3]. Thus answer to the first query is 4. We delete the added edge and process the next query.
- After adding the edge between nodes 4 and 7, the graph contains a cycle of nodes [4,2,1,3,7]. Thus answer to the second query is 5. We delete the added edge and process the next query.
- After adding the edge between nodes 2 and 3, the graph contains a cycle of nodes [2,1,3]. Thus answer to the third query is 3. We delete the added edge.

Example 2:

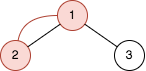
Input: n = 2, queries = [[1,2]]
Output: [2]
Explanation: The diagram above shows the tree of 22 - 1 nodes. Nodes colored in red describe the nodes in the cycle after adding the edge.
- After adding the edge between nodes 1 and 2, the graph contains a cycle of nodes [2,1]. Thus answer for the first query is 2. We delete the added edge.

Constraints:

• 2 <= n <= 30
• m == queries.length
• 1 <= m <= 105
• queries[i].length == 2
• 1 <= ai, bi <= 2n - 1
• ai != bi