2583. Divide Nodes Into the Maximum Number of Groups

You are given a positive integer n representing the number of nodes in an undirected graph. The nodes are labeled from 1 to n.

You are also given a 2D integer array edges, where edges[i] = [ai, bi] indicates that there is a bidirectional edge between nodes ai and bi. Notice that the given graph may be disconnected.

Divide the nodes of the graph into m groups (1-indexed) such that:

• Each node in the graph belongs to exactly one group.
• For every pair of nodes in the graph that are connected by an edge [ai, bi], if ai belongs to the group with index x, and bi belongs to the group with index y, then |y - x| = 1.

Return the maximum number of groups (i.e., maximum m) into which you can divide the nodes. Return -1 if it is impossible to group the nodes with the given conditions.

Example 1:

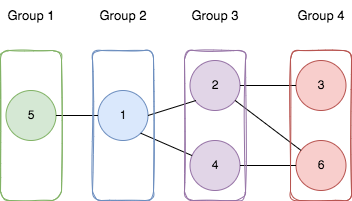
Input: n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]
Output: 4
Explanation: As shown in the image we:
- Add node 5 to the first group.
- Add node 1 to the second group.
- Add nodes 2 and 4 to the third group.
- Add nodes 3 and 6 to the fourth group.
We can see that every edge is satisfied.
It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied.

Example 2:

Input: n = 3, edges = [[1,2],[2,3],[3,1]]
Output: -1
Explanation: If we add node 1 to the first group, node 2 to the second group, and node 3 to the third group to satisfy the first two edges, we can see that the third edge will not be satisfied.
It can be shown that no grouping is possible.

Constraints:

• 1 <= n <= 500
• 1 <= edges.length <= 104
• edges[i].length == 2
• 1 <= ai, bi <= n
• ai != bi
• There is at most one edge between any pair of vertices.