3218. Find Number of Coins to Place in Tree Nodes

You are given an undirected tree with n nodes labeled from 0 to n - 1, and rooted at node 0. You are given a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

You are also given a 0-indexed integer array cost of length n, where cost[i] is the cost assigned to the ith node.

You need to place some coins on every node of the tree. The number of coins to be placed at node i can be calculated as:

• If size of the subtree of node i is less than 3, place 1 coin.
• Otherwise, place an amount of coins equal to the maximum product of cost values assigned to 3 distinct nodes in the subtree of node i. If this product is negative, place 0 coins.

Return an array coin of size n such that coin[i] is the number of coins placed at node i.

Example 1:

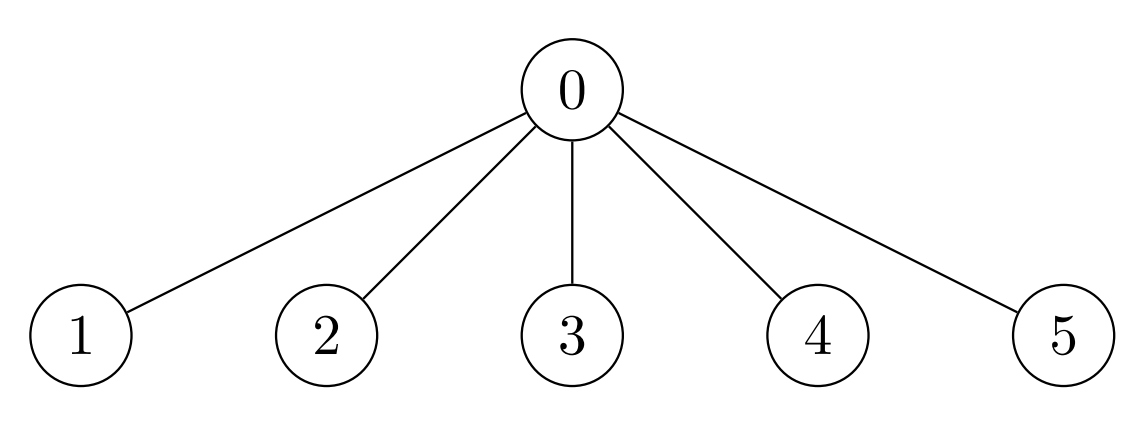
Input: edges = [[0,1],[0,2],[0,3],[0,4],[0,5]], cost = [1,2,3,4,5,6]
Output: [120,1,1,1,1,1]
Explanation: For node 0 place 6 * 5 * 4 = 120 coins. All other nodes are leaves with subtree of size 1, place 1 coin on each of them.

Example 2:

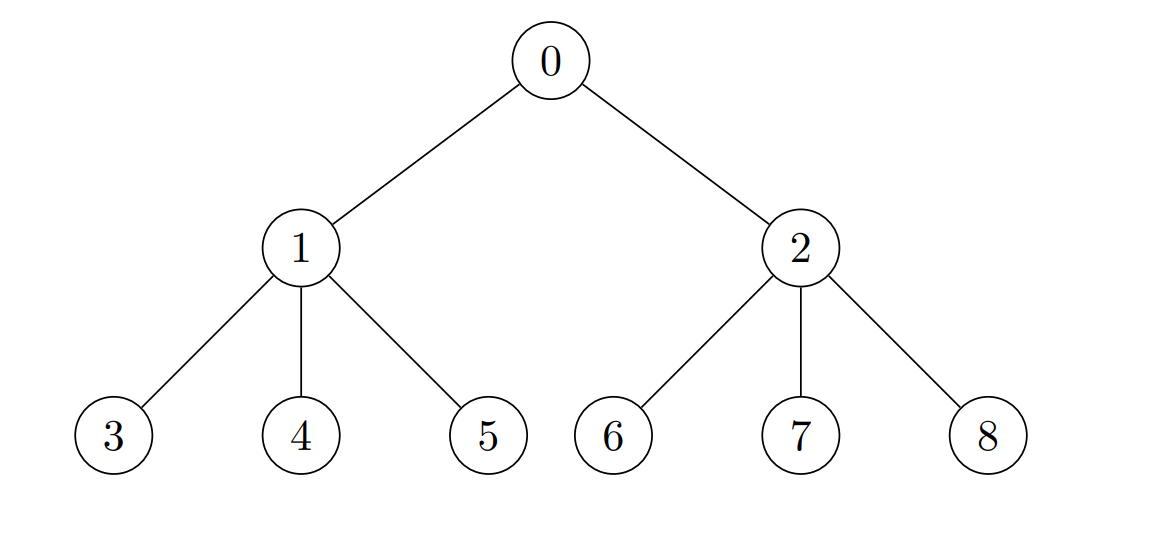
Input: edges = [[0,1],[0,2],[1,3],[1,4],[1,5],[2,6],[2,7],[2,8]], cost = [1,4,2,3,5,7,8,-4,2]
Output: [280,140,32,1,1,1,1,1,1]
Explanation: The coins placed on each node are:
- Place 8 * 7 * 5 = 280 coins on node 0.
- Place 7 * 5 * 4 = 140 coins on node 1.
- Place 8 * 2 * 2 = 32 coins on node 2.
- All other nodes are leaves with subtree of size 1, place 1 coin on each of them.

Example 3:

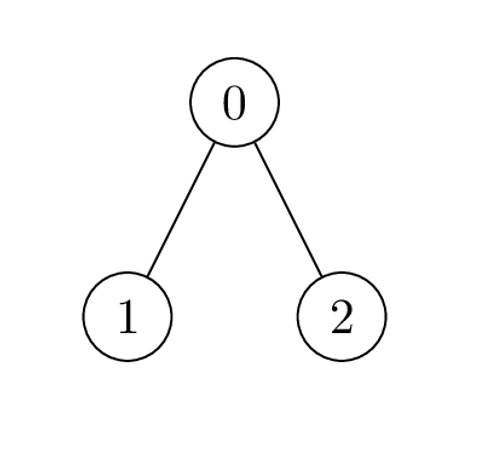
Input: edges = [[0,1],[0,2]], cost = [1,2,-2]
Output: [0,1,1]
Explanation: Node 1 and 2 are leaves with subtree of size 1, place 1 coin on each of them. For node 0 the only possible product of cost is 2 * 1 * -2 = -4. Hence place 0 coins on node 0.

Constraints:

• 2 <= n <= 2 * 104
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• cost.length == n
• 1 <= |cost[i]| <= 104
• The input is generated such that edges represents a valid tree.