Company-Wise Interview Questions

You are given a m x n matrix grid consisting of non-negative integers.

In one operation, you can increment the value of any grid[i][j] by 1.

Return the minimum number of operations needed to make all columns of grid strictly increasing.

Example 1:

Input: grid = [[3,2],[1,3],[3,4],[0,1]]

Output: 15

Explanation:

To make the 0^th column strictly increasing, we can apply 3 operations on grid[1][0], 2 operations on grid[2][0], and 6 operations on grid[3][0].
To make the 1^st column strictly increasing, we can apply 4 operations on grid[3][1].

Example 2:

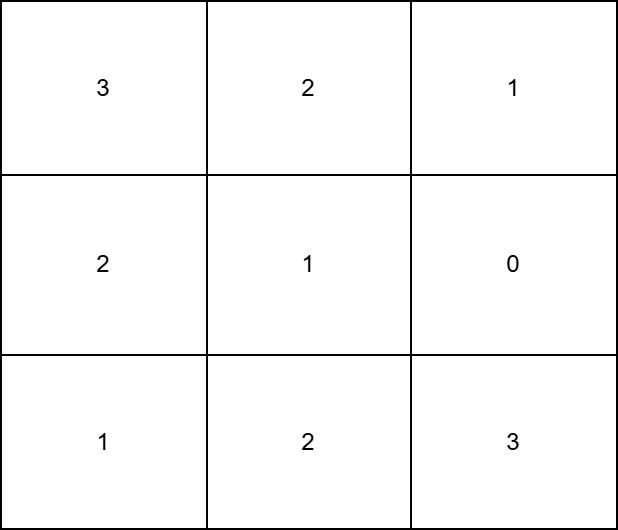
Input: grid = [[3,2,1],[2,1,0],[1,2,3]]

Output: 12

Explanation:

To make the 0^th column strictly increasing, we can apply 2 operations on grid[1][0], and 4 operations on grid[2][0].
To make the 1^st column strictly increasing, we can apply 2 operations on grid[1][1], and 2 operations on grid[2][1].
To make the 2^nd column strictly increasing, we can apply 2 operations on grid[1][2].

Constraints:

Hint 1

<code>grid[i + 1][j]</code> must be at least equal to <code>grid[i][j] + 1<code>.

Hint 2

Iterate on <code>i</code> in increasing order, and set <code>grid[i + 1][j] = max(grid[i][j]+1, grid[i + 1][j])<code>.

Acceptance

72.4%

Submissions

49,768

Accepted

36,024

3691. Minimum Operations to Make Columns Strictly Increasing