2409. Number of Increasing Paths in a Grid

You are given an m x n integer matrix grid, where you can move from a cell to any adjacent cell in all 4 directions.

Return the number of strictly increasing paths in the grid such that you can start from any cell and end at any cell. Since the answer may be very large, return it modulo 109 + 7.

Two paths are considered different if they do not have exactly the same sequence of visited cells.

Example 1:

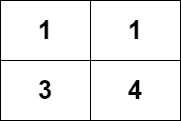
Input: grid = [[1,1],[3,4]]
Output: 8
Explanation: The strictly increasing paths are:
- Paths with length 1: [1], [1], [3], [4].
- Paths with length 2: [1 -> 3], [1 -> 4], [3 -> 4].
- Paths with length 3: [1 -> 3 -> 4].
The total number of paths is 4 + 3 + 1 = 8.

Example 2:

Input: grid = [[1],[2]]
Output: 3
Explanation: The strictly increasing paths are:
- Paths with length 1: [1], [2].
- Paths with length 2: [1 -> 2].
The total number of paths is 2 + 1 = 3.

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 1000
• 1 <= m * n <= 105
• 1 <= grid[i][j] <= 105